主成分分析(PCA)是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关变量称为主成分,它们是观测变量的线性组合。如第一主成分为:
PC1=a1X1=a2X 2+…+akXk
它是k个观测变量的加权组合,对初始变量集的方差解释性最大。第二主成分也是初始变量的线性组合,对方差的解释性排第二,同时与第一主成分正交(不相关)。后面每一个主成分都最大化它对方差的解释程度,同时与之前所有的主成分都正交。
PCA分析模型如下图: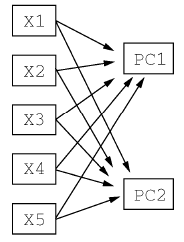
例如如下数据的PCA分析:
学生身体4 项指标的主成份分析1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31学生序号 x1身高 x2体重 x3胸围 x4坐高
1 148 41 72 78
2 139 34 71 76
3 160 49 77 86
4 149 36 67 79
5 159 45 80 86
6 142 31 66 76
7 153 43 76 83
8 150 43 77 79
9 151 42 77 80
10 139 31 68 74
11 140 29 64 74
12 161 47 78 84
13 158 49 78 83
14 140 33 67 77
15 137 31 66 73
16 152 35 73 79
17 149 47 82 79
18 145 35 70 77
19 160 47 74 87
20 156 44 78 85
21 151 42 73 82
22 147 38 73 78
23 157 39 68 80
24 147 30 65 75
25 157 48 80 88
26 151 36 74 80
27 144 36 68 76
28 141 30 67 76
29 139 32 68 73
30 148 38 70 78
数据读入R软件
1 | > d=read.table("clipboard",header=T) |
原始数据标准化1
> sd=scale(d)
标准化数据展示1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38> sd
x1身高 x2体重 x3胸围 x4坐高
[1,] -0.1366952 0.35602486 -0.04530114 -0.31999814
[2,] -1.3669516 -0.72752905 -0.23944887 -0.78828809
[3,] 1.5036468 1.59437218 0.92543751 1.55316168
[4,] 0.0000000 -0.41794222 -1.01603978 -0.08585316
[5,] 1.3669516 0.97519852 1.50788070 1.55316168
[6,] -0.9568661 -1.19190930 -1.21018751 -0.78828809
[7,] 0.5467806 0.66561169 0.73128978 0.85072675
[8,] 0.1366952 0.66561169 0.92543751 -0.08585316
[9,] 0.2733903 0.51081827 0.92543751 0.14829182
[10,] -1.3669516 -1.19190930 -0.82189205 -1.25657805
[11,] -1.2302564 -1.50149613 -1.59848297 -1.25657805
[12,] 1.6403419 1.28478535 1.11958524 1.08487173
[13,] 1.2302564 1.59437218 1.11958524 0.85072675
[14,] -1.2302564 -0.88232247 -1.01603978 -0.55414311
[15,] -1.6403419 -1.19190930 -1.21018751 -1.49072302
[16,] 0.4100855 -0.57273564 0.14884659 -0.08585316
[17,] 0.0000000 1.28478535 1.89617616 -0.08585316
[18,] -0.5467806 -0.57273564 -0.43359660 -0.55414311
[19,] 1.5036468 1.28478535 0.34299432 1.78730666
[20,] 0.9568661 0.82040510 1.11958524 1.31901671
[21,] 0.2733903 0.51081827 0.14884659 0.61658177
[22,] -0.2733903 -0.10835539 0.14884659 -0.31999814
[23,] 1.0935613 0.04643802 -0.82189205 0.14829182
[24,] -0.2733903 -1.34670271 -1.40433524 -1.02243307
[25,] 1.0935613 1.43957876 1.50788070 2.02145164
[26,] 0.2733903 -0.41794222 0.34299432 0.14829182
[27,] -0.6834758 -0.41794222 -0.82189205 -0.78828809
[28,] -1.0935613 -1.34670271 -1.01603978 -0.78828809
[29,] -1.3669516 -1.03711588 -0.82189205 -1.49072302
[30,] -0.1366952 -0.10835539 -0.43359660 -0.31999814
attr(,"scaled:center")
x1身高 x2体重 x3胸围 x4坐高
149.00000 38.70000 72.23333 79.36667
attr(,"scaled:scale")
x1身高 x2体重 x3胸围 x4坐高
7.315548 6.460223 5.150717 4.270858
读取标准化数据1
> d=read.table("clipboard",header=T)
主成分分析1
> pca=princomp(d,cor=T)
碎石图1
2> screeplot(pca,type="line",main="碎石图",lwd=2)
>
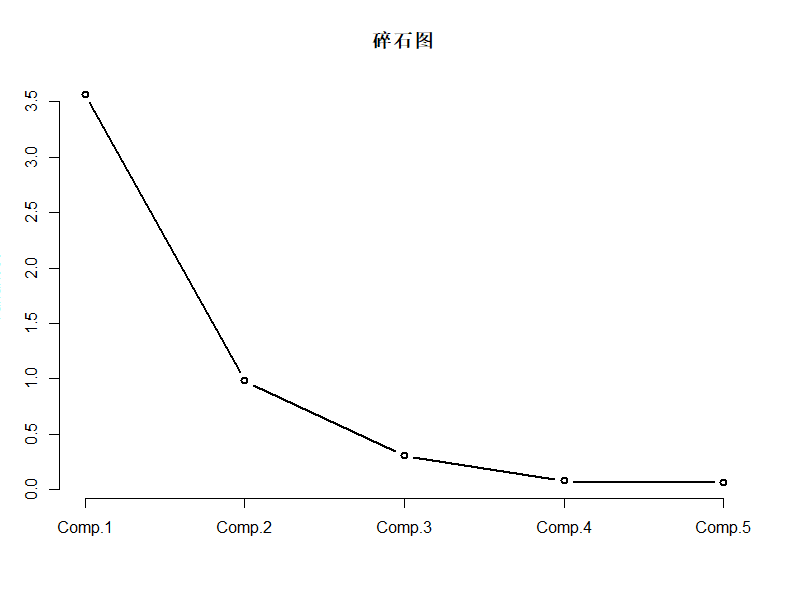
主成分1贡献率较高
求相关矩阵1
> dcor=cor(d)
输出1
2
3
4
5
6> dcor
x1身高 x2体重 x3胸围 x4坐高
x1身高 1.0000000 0.8631621 0.7321119 0.9204624
x2体重 0.8631621 1.0000000 0.8965058 0.8827313
x3胸围 0.7321119 0.8965058 1.0000000 0.7828827
x4坐高 0.9204624 0.8827313 0.7828827 1.0000000
求相关矩阵的特征向量 特征值1
> deig=eigen(dcor)
输出1
2
3
4
5
6
7
8
9>deig
$values
[1] 3.54109800 0.31338316 0.07940895 0.06610989
$vectors
[,1] [,2] [,3] [,4]
[1,] -0.4969661 0.5432128 -0.4496271 0.5057471
[2,] -0.5145705 -0.2102455 -0.4623300 -0.6908436
[3,] -0.4809007 -0.7246214 0.1751765 0.4614884
[4,] -0.5069285 0.3682941 0.7439083 -0.2323433
输出特征值1
2
3
4
5> deig$values
[1] 3.54109800 0.31338316 0.07940895 0.06610989
> sumeigv=sum(deig$values)
> sumeigv
[1] 4
求前2个主成分的累积方差贡献率1
2
3
4> sum(deig$value[1:2])/4
[1] 0.9636203
> sum(deig$value[1:1])/4
[1] 0.8852745
第一主成份有88.53%的方差贡献率,前两个主成份累计贡献率更高达96.36%,故只需前两个主成份就能很好地概括这组数据.
输出前两个主成分的载荷系数(特征向量)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22> pca$loadings[,1:2]
Comp.1 Comp.2
x1身高 -0.4969661 0.5432128
x2体重 -0.5145705 -0.2102455
x3胸围 -0.4809007 -0.7246214
x4坐高 -0.5069285 0.3682941
-----------------------------------------
z1=-0.4969661 x1+-0.5145705 x2 +-0.4809007x3+-0.5069285x4
z2=0.5432128 x1+-0.2102455 x2 +-0.7246214x3+0.3682941x4
z= 3.54109800/4 z1 + 0.31338316/4 z2=0.8852745 z1 +0.07834579 Z2
=0.8852745(-0.4969661 x1+-0.5145705 x2 +-0.4809007x3+-0.5069285x4)
+0.07834579 (0.5432128 x1+-0.2102455 x2 +-0.7246214x3+0.3682941x4)
-----------------------------------------
计算主成分C1和C2的系数b1 和b2:1
2
3> deig$values[1]/4;deig$values[2]/4
[1] 0.8852745
[1] 0.07834579
综合得分函数C 为:1
C=(b1*C1+b2*C2)/(b1+b2)=0.9187*C1+0.0813*C2
输出前2 个主成分的得分1
> s=pca$scores[,1:2]
计算综合得分1
2
3
4
5
6
7
8> c=s[1:30,1]*0.918696+s[1:30,2]*0.0813
> s[1:30,1]
[1] 0.06990950 1.59526340 -2.84793151 0.75996988 -2.73966777 2.10583168
[7] -1.42105591 -0.82583977 -0.93464402 2.36463820 2.83741916 -2.60851224
[13] -2.44253342 1.86630669 2.81347421 0.06392983 -1.55561022 1.07392251
[19] -2.52174212 -2.14072377 -0.79624422 0.28708321 -0.25151075 2.05706032
[25] -3.08596855 -0.16367555 1.37265053 2.16097778 2.40434827 0.50287468
输出综合得分信息1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33> cbind(s,c)
Comp.1 Comp.2 c
[1,] 0.06990950 -0.23813701 0.04486504
[2,] 1.59526340 -0.71847399 1.40715017
[3,] -2.84793151 0.38956679 -2.58471151
[4,] 0.75996988 0.80604335 0.76371262
[5,] -2.73966777 0.01718087 -2.51552502
[6,] 2.10583168 0.32284393 1.96086635
[7,] -1.42105591 -0.06053165 -1.31043961
[8,] -0.82583977 -0.78102576 -0.82219309
[9,] -0.93464402 -0.58469242 -0.90618922
[10,] 2.36463820 -0.36532199 2.14268298
[11,] 2.83741916 0.34875841 2.63507969
[12,] -2.60851224 0.21278728 -2.37913015
[13,] -2.44253342 -0.16769496 -2.25757928
[14,] 1.86630669 0.05021384 1.71865087
[15,] 2.81347421 -0.31790107 2.55888214
[16,] 0.06392983 0.20718448 0.07557617
[17,] -1.55561022 -1.70439674 -1.56770034
[18,] 1.07392251 -0.06763418 0.98110965
[19,] -2.52174212 0.97274301 -2.23763039
[20,] -2.14072377 0.02217881 -1.96487123
[21,] -0.79624422 0.16307887 -0.71824807
[22,] 0.28708321 -0.35744666 0.23468178
[23,] -0.25151075 1.25555188 -0.12898555
[24,] 2.05706032 0.78894494 1.95395431
[25,] -3.08596855 -0.05775318 -2.83976229
[26,] -0.16367555 0.04317932 -0.14685759
[27,] 1.37265053 0.02220972 1.26285420
[28,] 2.16097778 0.13733233 1.99644676
[29,] 2.40434827 -0.48613137 2.16934265
[30,] 0.50287468 0.14734317 0.47396795
>
排序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30[11,] 2.83741916 0.34875841 2.63507969
[15,] 2.81347421 -0.31790107 2.55888214
[29,] 2.40434827 -0.48613137 2.16934265
[10,] 2.3646382 -0.36532199 2.14268298
[28,] 2.16097778 0.13733233 1.99644676
[6,] 2.10583168 0.32284393 1.96086635
[24,] 2.05706032 0.78894494 1.95395431
[14,] 1.86630669 0.05021384 1.71865087
[2,] 1.5952634 -0.71847399 1.40715017
[27,] 1.37265053 0.02220972 1.2628542
[18,] 1.07392251 -0.06763418 0.98110965
[4,] 0.75996988 0.80604335 0.76371262
[30,] 0.50287468 0.14734317 0.47396795
[22,] 0.28708321 -0.35744666 0.23468178
[16,] 0.06392983 0.20718448 0.07557617
[1,] 0.0699095 -0.23813701 0.04486504
[23,] -0.25151075 1.25555188 -0.12898555
[26,] -0.16367555 0.04317932 -0.14685759
[21,] -0.79624422 0.16307887 -0.71824807
[8,] -0.82583977 -0.78102576 -0.82219309
[9,] -0.93464402 -0.58469242 -0.90618922
[7,] -1.42105591 -0.06053165 -1.31043961
[17,] -1.55561022 -1.70439674 -1.56770034
[20,] -2.14072377 0.02217881 -1.96487123
[19,] -2.52174212 0.97274301 -2.23763039
[13,] -2.44253342 -0.16769496 -2.25757928
[12,] -2.60851224 0.21278728 -2.37913015
[5,] -2.73966777 0.01718087 -2.51552502
[3,] -2.84793151 0.38956679 -2.58471151
[25,] -3.08596855 -0.05775318 -2.83976229
